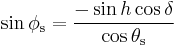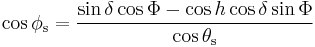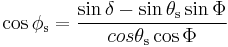Solar azimuth angle
The solar azimuth angle is the azimuth angle of the sun. It is most often defined as the angle from due north in a clockwise direction.
It can be calculated in various way. In different times, it has been explained in different ways. It can be calculated, to a good approximation, using the following formula, however angles should be interpreted with care due to the inverse sine, i.e. x = sin−1(y) has more than one solution, only one of which will be correct.
The following two formulas can also be used to approximate the solar azimuth angle, however because these formulas utilize cosine, the azimuth angle will always be positive, and therefore, should be interpreted as the angle less than 180 degrees when the hour angle, h, is negative (morning) and the angle greater than 180 degrees when the hour angle, h, is positive (afternoon).
The previous formulas use the following terminology:
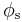 is the solar azimuth angle
is the solar azimuth angle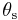 is the solar elevation angle
is the solar elevation angle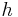 is the hour angle of the present time
is the hour angle of the present time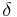 is the current sun declination
is the current sun declination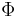 is the local latitude[1]
is the local latitude[1]
Contents |
Solar elevation angle
Sun height, height angle, solar altitude angle or elevation (gS) is the angle between a line that points from the site towards the centre of the sun, and the horizon. The zenith angle is the opposite angle to the sun height (90° – gS). At a sun height of 90°, the sun is at the zenith and the zenith angle is therefore zero.[2]
See also
References
- ^ The formula is based on geocentric latitude, which differs from geographic latitude by less than 12 minutes of arc.
- ^ http://www.volker-quaschning.de/articles/fundamentals1/index_e.html
External links
- Solar Position Calculators by National Renewable Energy Laboratory (NREL)
- An Excel workbook with VBA functions for solar azimuth, solar elevation, dawn, sunrise, solar noon, sunset, and dusk, by Greg Pelletier, translated from NOAA's online calculators for solar position and sunrise/sunset
- An Excel workbook with a solar position and solar radiation time-series calculator, by Greg Pelletier
- Free on-line tool to estimate the position of the sun with three different algorithms.